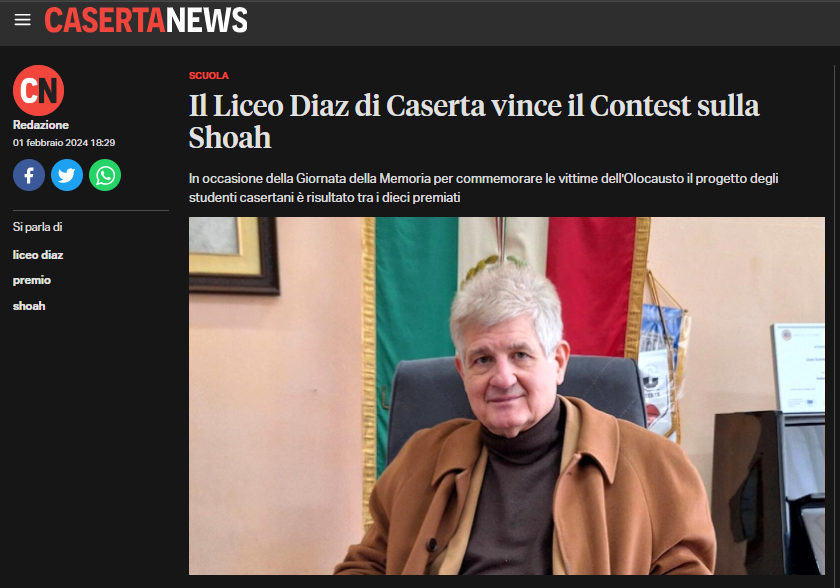







Vincere un Premio di Fisica trattando il tema di genere.
DONNE D’IMPATTO : una scienziata cinese Chien Shiung Wu
Il Diaz è sul Nuovo Saggiatore!
Un plauso alle nostre docenti Anna Di Nocera e Stefania Zampella che hanno saputo motivare i ragazzi,
suscitare il loro interesse e lasciar libera la creatività.

Quattro studenti del Diaz dalla seconda alla quarta: Rossella Arnese (3R), Giovanni Piombino (4L), Lorenzo Farro (4E) e Ida Qu (2G), supportati nel lavoro ed accompagnati dalle prof.sse Anna Di Nocera e Stefania Zampella, sono stati premiati al concorso “ DONNE E RICERCA IN FISICA: tra stereotipi di genere e professioni del futuro “ con Menzione Speciale per l’originalità ed il lavoro di gruppo di un video dal titolo “Donne d’Impatto”, centrato sulla vita personale e professionale di una scienziata cinese Chien Shiung Wu, mancato premio Nobel per la fisica negli anni 50. La premiazione è avvenuta il 29 maggio 2023 presso la Sala Congressi del CNR a Roma, in occasione del centenario del CNR, in presenza di rappresentanti delle istituzioni e del mondo scientifico. Grazie al riconoscimento del lavoro dei ragazzi il Liceo Diaz ha avuto accesso all’associazione gratuita per l’anno 2023 alla Società Italiana di Fisica (SIF) ed a tutti i contenuti on line messi a disposizione dal SIF e riceverà la copia cartacea della rivista Il Nuovo Saggiatore per il biennio 2023-24.
IL LAVORO PRESENTATO